Author: Yun Mak
Peer reviewers: Aidan Burrell, Chris Nickson
Nuts and Bolts of EBM Part 4
This study says this, that study says that. Wouldn’t it be great if we could somehow combine trials together to try to get closer to the truth?
We can.
However, as clinicians and burgeoning connoisseurs of ‘the evidence’, there are a few things we need to know to avoid being led astray.
Q1. What is a systematic review and what is a meta-analysis… How do they differ?
A systematic review is review of a clearly formulated question using systematic and explicit methods to identify, select and critically appraise all relevant research. Data is collected and analysed from all the studies that are included in the review.
Meta-analysis, on the other hand, is the process of using statistical methods to combine the samples and analyse the results of the included studies. The overall sample size is increased, thereby improving the statistical power of the analysis as well as the precision of the estimates of treatment effects.
Q2. What are the steps involved in performing a systematic review and meta-analysis?
In brief, the 7 key steps involved are:
- Formulate a review question
- Perform a comprehensive search of the literature for published AND unpublished evidence
- Select studies for inclusion
- Critically appraise studies
- Synthesize the findings from individual studies
- Combine study results (meta-analysis)
- Interpret results and provide recommendations
Q3. What are the benefits and limitations os systematic review and meta-analysis?
A systematic review of well-performed randomised controlled trials is regarded as the highest level within the evidence hierarchy (see Levels and Grades of Evidence in the LITFL CCC).
Benefits
- Increases statistical power (chance of detecting a real effect as statistically significant if it exists)
- Increases precision (estimation of intervention effect size)
- Summarises contemporary literature on a topic
- May help resolve conflicting studies
- Starting point for clinical guidelines and policy
- Identifies topics for further research
- Avoids Simpson’s paradox (if populations are separated in parallel into a set of descriptive categories, the population with the highest overall incidence may paradoxically have a lower incidence within each such category… this is explained much more simply on Youtube)
Limitations
- Limited by the quality of studies that comprise the review… aka “garbage in, garbage out”, biases present in individual studies may be compounded by meta-analysis and may appear to have more credibility as a result
- Difficult when there is only a small number or trials, or small patient numbers
- Difficult when one trial provides the majority of sample size
- Poor quality analysis can have misleading findings
- Susceptible to reporting bias / publication bias of individual studies
- Cannot combine ‘apples with oranges’ – cannot combine studies that are too clinically diverse in terms of intervention, comparison or outcomes.
Q4. Describe a useful approach to critically appraise a systematic review and meta-analysis?
The University of Oxford Centre for Evidence-Based Medicine has a suggested method for critical appraisal of systematic review and meta-analysis. The Worksheet can be found here: http://www.cebm.net/wp-content/uploads/2014/06/SYSTEMATIC-REVIEW.docx
In summary, the review should be appraised using the PICO format and fulfil all 5 criteria of the FAITH tool.
- What question (PICO) did the review address?
- FAITH tool:
- FIND all relevant studies
- APPRAISE the use of appropriate inclusion criteria
- INCLUDED all valid studies
- TOTAL pooling of similar results
- HETEROGENEITY and inconsistency of PICOs and results
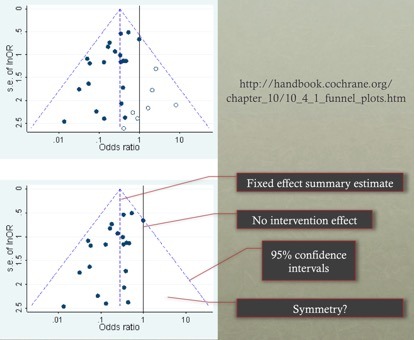
Q5. What are funnel plots and how are they interpreted?
A funnel plot is a scatter plot of the effect estimates from individual studies against some measure of each study’s size or precision. Traditionally the funnel plot was used to assess for the presence of publication bias or selective outcome reporting (relevant to the F part of the FAITH tool).
The standard error of the effect estimate is often chosen as a measure of the accuracy of the predictions of the study. This is plotted on the vertical axis with a reversed scale that places the larger, most powerful studies towards the top.
The effect estimates from smaller studies should scatter more widely at the bottom, with the spread narrowing among larger studies.
Orientation:
- The central dashed line is the fixed effect summary estimate.
- The outer dashed lines indicate the triangular region within which 95% of studies are expected to lie in the absence of both bias and heterogeneity (fixed effect summary log odds ratio±1.96×standard error of summary log odds ratio).
- The solid vertical line corresponds to no intervention effect.
- A triangle centred on a fixed effect summary estimate and extending 1.96 standard errors either side will include about 95% of studies if no bias is present and the fixed effect assumption (that the true treatment effect is the same in each study) is valid.
Interpretation:
- The funnel plot may recommend caution in interpretation due to the presence of asymmetry or failure of the confidence intervals to contain 95% of the studies (both may suggest potential bias or heterogeneity).
- Asymmetry traditionally was thought due to bias towards favourable treatment effects due to the lack of published results of no difference. However there are other possible sources of asymmetry:
- Reporting biases
- publication bias (delayed publication or location bias, e.g. foreign language papers)
- selective outcome reporting
- selective analysis reporting
- Spuriously inflated effects in smaller studies
- poor methodological design
- fraud
- inadequate analysis
- True heterogeneity
- Artefact (in some contexts, sampling variation can lead to an association between the intervention effect and its standard error)
- Chance
- Reporting biases
NB. The article by Sterne (BMJ 2011) summarizes funnel plots and is where the CICM exam sought their answer for SAQ 2014.2 Q13.
Q6. What are forest plots and how are they interpreted?
A forest plot is a diagram that shows information from the individual studies that went into the meta-analysis and an estimate of the overall results (relevant to the T and H parts of the FAITH tool). Interpreting a forest plot requires knowledge of the two stages of performing meta-analysis.
The first stage involves the calculation of a measure of treatment effect with its 95% confidence intervals for each individual study. The second stage involves calculation of an overall treatment effect as a weighted average of the individual studies.
Greater weights are given to the results from studies that provide more information, because they are likely closer to the “true effect” we are trying to estimate. The weights are often the inverse of the variance (the square of the standard error) of the treatment effect, which relates closely to sample size.
Orientation:
- The first authors and year of the primary studies included are on the left.
- The solid vertical line corresponds to no intervention effect (OR = 1.0).
- The black squares represent the odds ratios of the individual studies, and the horizontal lines their 95% confidence intervals. The area of the black squares reflects the weight each trial contributes in the meta-analysis. If the 95% confidence interval crosses the no intervention effect, then the study results were not statistically significant (p>0.05).
- The overall treatment effect (calculated as a weighted average of the individual ORs) from the meta-analysis is represented as a diamond. The centre of the diamond represents the combined intervention effect, and the horizontal tips represent the 95% confidence intervals.
Interpretation:
- The overall results of the meta-analysis – the centre of the diamond represents the overall treatment effect. If the diamond reaches the no intervention effect, then the overall treatment effect is not statistically significant.
- Visual assessment of heterogeneity – the vertical dashed line runs through the centre of the diamond. If this dashed line crosses the 95% confidence intervals of each individual study, then there is no significant heterogeneity.
- Random-effects vs. fixed effects meta-analysis – the forest plot will state if the meta-analysis was performed using fixed- or random-effects. In a fixed effects model, we assume the true effect size for all studies is identical (so a large study will heavily influence the results) whereas, in a random effects model, we assess the mean of a distribution of effects, so each study is given more equal representation in the study estimate. Due to between-study heterogeneity, the true effect may differ from study to study and so a random-effects model is most often the appropriate method to use (ie. if fixed is used, heterogeneity will make it difficult to interpret).
NB. Forest plot interpretation was assessed by CICM in SAQ 2015.1 Q8.
Q7. How is heterogeneity represented in a meta-analysis?
Heterogeneity (or statistical heterogeneity) refers to variability in the intervention effects being evaluated in different studies included in a systematic review as a consequence of clinical or methodological diversity, or both, among the studies. This becomes manifest as the observed intervention effects being more different from each other than one would expect due to random error (chance) alone.
- clinical diversity – variability in the participants, interventions and outcomes studied may be described as
- methodological diversity -variability in study design and risk of bias
Heterogeneity (Cochran Q test, χ2)
- A small P value means the null hypothesis (of study homogeneity) should be rejected – and the studies should not be combined. Unfortunately, the power of this test is relatively low when there are few studies (which is common).
- Traditionally a P value of 0.05 is used, however, this may be lower or higher (0.10) at the authors’ discretion.
Inconsistency (I2)
- Some believe that because study variability is unavoidable, inconsistency is a more useful marker to assess the ability to combine these into meta-analysis. Inconsistency quantifies the percentage of variability between studies that is due to heterogeneity rather than due to chance.
- There is no value considered too high – the original description suggested I2 values of 25%, 50% and 75% indicated low, moderate and high levels of heterogeneity.
References and links
- Centre for Evidence-Based Medicine, University of Oxford – Systematic Reviews Critical Appraisal Worksheet. [Cited 27 July 2016] Available from URL: http://www.cebm.net/critical-appraisal/
- Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 (March 2011) [Cited 27 July 2016] Available from URL: http://handbook.cochrane.org/
- Dartmouth College Library Research Guides Systematic Reviews: Planning, Writing, and Supporting. [Cited 27 July 2016] Available from URL: http://researchguides.dartmouth.edu/sys-reviews
- Egger M, Davey Smith G, Schneider M, Minder C. Bias in meta-analysis detected by a simple, graphical test. BMJ (Clinical research ed.). 315(7109):629-34. 1997. [pubmed]
- Nickson CP. Levels and Grades of Evidence. Lifeinthefastlane.com. [Cited 27 July 2016] Available from URL: http://lifeinthefastlane.com/ccc/levels-and-grades-of-evidence/
- Reade MC, Delaney A, Bailey MJ, Angus DC. Bench-to-bedside review: avoiding pitfalls in critical care meta-analysis–funnel plots, risk estimates, types of heterogeneity, baseline risk and the ecologic fallacy. Critical care (London, England). 12(4):220. 2008. [pubmed]
- Sterne JA, Sutton AJ, Ioannidis JP. Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. BMJ (Clinical research ed.). 343:d4002. 2011. [pubmed]